摘要
这篇论文总体上介绍了cilqr在自动驾驶路径规划中的应用,主要的贡献是提供了一种方法使ilqr可以处理约束问题
正文
问题构建
ILQR的前世今生
文章通过三个问题来构建了整个ilqr算法的求解过程:

问题一是一个通用的轨迹规划的最优问题,需要规划出一条满足动力学约束、非线性的状态约束(通常是障碍处理)、非线性的输入约束(通常是受限于执行机构)以及能够处理非线性的cost(包括终端cost)
文章中提出这个问题可以通过sqp来求解,但在自动驾驶中其效率不如通过ilqr来求解

文章提供了一个标准的ilqr问题,不难看出这个问题中的cost是线性的cost且只能处理一个等式约束,无法显式的处理其他约束。
这个ilqr问题后面会开一个帖子单独讲讲,在这里我们将他理解为通过多次lqr迭代来逼近最优解的一种方法,那么为什么要通过这样的多次迭代来逼近而不是直接求解呢?很显然3a中的系统动力学方程是非线性的,这就导致无法直接通过李卡迪方程来求解。如果想通过lqr问题来求解这个问题就要对非线性的动力学方程进行展开,一旦进行这样的展开势必会引入误差,所以ilqr是通过不断地收敛这个误差(类似高斯牛顿法)的方式来求解。
文章中给出ilqr的算法思路

前向就是通过求解出的u前向传递状态直到规定步数,反向就是通过上一次求解出的状态作为参考再次求解一系列deltax和deltau。
那么按照这样的步骤,我们在每个时间步骤所面临的问题就是一个标准的lqr问题(如4中所示),这就引出了问题3:

标准lqr问题想必能读到这里的人应该都有所了解这里不再赘述, 通过求解李卡迪方程可以得到最优解(总体上看是局部的最优解)
CILQR(Constrained Iterative LQR)
不难看出,想要通过ILQR框架(也就是问题二)去解决问题一还有两个问题需要解决:
1.怎么处理非线性的成本函数
2.怎么让这套ilqr算法可以处理约束呢?
对于问题1,文章将非线性的cost进行了二阶展开为二次型

而对于等式约束,在上面的ilqr中我们已经讨论过要将其进行线性化,也就是进行一阶展开

那么f_k经过线性化后,将f_k < 0 这个不等式约束转换为cost呢?文章使用了障碍函数来处理状态的不等式约束,障碍函数的定义如下

不难观察,这个函数会极大地惩罚f_k > 0的值,这样就可以将非线性的约束转换为cost,但这个cost并不符合二次型,所以引入步骤4

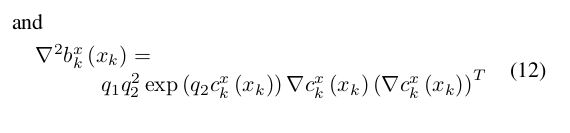
将cost也转换成二次型行驶,至此已经将问题一转换成了一个无约束的ilqr求解问题,再根据ilqr算法,不断地迭代标准lqr问题,即可对轨迹进行优化
模型设计
经过前面的努力,终于将要解决的问题模型变成了这样:

除了13c和13d以外似乎和问题一没差,现在的任务就是将13c 和 13d修改为不等式形式。13c是为了保证静态障碍物的约束,13d为输入的可行域,难点在于如何表示障碍物既能有效表示障碍,同时还能转换为简单的不等式约束


Comments NOTHING