最近工程上调试lqr相关的算法有些心烦，想再仔细推导一遍静静心，在网上搜索了一圈教程总觉得差点意思，决定自己详细的写一遍从lqr的通用解法一直到cilqr的求解，文章会保留所有几乎所有的推导步骤，甚至不会省略移项、矩阵转置等步骤以防读者跟丢，所以文章会显得比较冗长，但跟着拿笔推导一遍相信总会有收获。

LQR推导

对于LQR来说我们要解决的是一个有限时域下的最优问题：

$$\begin{matrix}
\min_{u}{x_N^TQ_Nx_x + \sum_{t = 1}^{N-1} x_t^TQ_tx_t + u_t^TR_tu_t}\\
st. x_{t+1} = A_tx_t + B_tu_t
\end{matrix}$$

为了求解这个最优问题，我们构建价值函数:

$$V_t(x_t) = \min_{u}{x_t^TQ_tx_t + u_t^TR_tu_t + V_{t+1}(x_{t+1})}$$

这里的$V_t(x_t) $所代表的具体含义为 $t $时刻一直到终端时刻，在使用最优解的情况下代价函数的最小值，这个概念很绕但很好理解，$ V_t $的两个部分一个是当前时刻的代价，一个是下个时刻的代价，不难看出这是一个递归函数，可以移植延伸到终端时刻$ N $。这个代价函数的设计在最优控制和强化学习中都很常见。我们的目标就是求解出这个最优的控制序列 $ u^* = {u^*_1, u^*_2, ..., u^*_N} $。在lqr中，控制量被设计为全状态反馈，也就是

$$ u^*_i = -K_ix_i $$

这里我们不讨论贝尔曼方程这些概念性的东西，只从求解的思路来说，可以发现每一个时刻的代价函数都要依赖下一时刻的值，这样的写法无法显示的给出代价函数和输入u的关系，所以我们的第一个任务是要求解出这个代价函数和最优输入 $ u^* $的显示表达。

从 $ V_t $的形式不能看出似乎只有终端时刻的代价不需要未来的信息很容易就可以写出他的显式表达：

$$V_N = x_N^TQ_Nx_N$$

这里我们给出一个推演性的结论，任意时刻的代价函数都可以写成以下形式：

$$ V_t = x_t^TP_tx_t $$

为什么得出这样的结论？因为代价函数是从终端代价推演回去的，当$V_N$是二次型时，$V_{N-1} = x_{N-1}^TQ_{N-1}x_{N-1} + (kx_{N-1})^TR_{N-1} (kx_{N-1}) +x_N^TQ_Nx_N $ 。显然这是状态的一系列线性变换，一定可以整理为二次型形式，同理这样一直递推回去每一个时刻都可以这样表达。

有了这样的结论我们就可以进一步的推导代价函数的递推公式，目标是让递推公式对$u_t$求导等于0时（也就是理论上的最优解）只与$P_t+1$和$x_t$有关，这样我们就可以通过终端的$P_N = Q_N$来一步一步递推回去求得每个时刻的最优解。

LaTeX

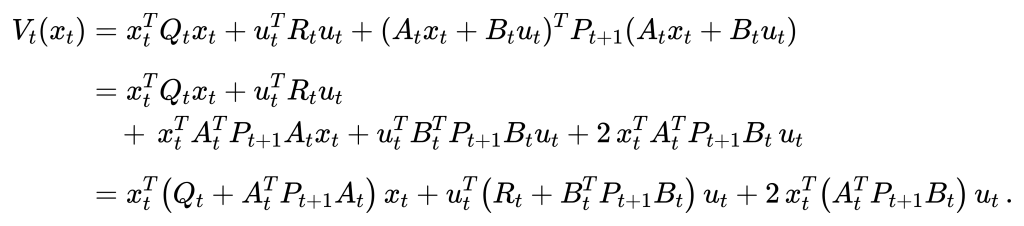
\begin{aligned}V_t(x_t)&= x_t^T Q_t x_t  + u_t^T R_t u_t  + (A_t x_t + B_t u_t)^T P_{t+1} (A_t x_t + B_t u_t)\\[6pt]&= x_t^T Q_t x_t  + u_t^T R_t u_t \\&\quad +\, x_t^T A_t^T P_{t+1} A_t x_t  + u_t^T B_t^T P_{t+1} B_t u_t + 2\,x_t^T A_t^T P_{t+1} B_t\,u_t \\[6pt]&= x_t^T \bigl(Q_t + A_t^T P_{t+1} A_t\bigr)\,x_t  + u_t^T \bigl(R_t + B_t^T P_{t+1} B_t\bigr)\,u_t  + 2\,x_t^T\bigl(A_t^T P_{t+1} B_t\bigr)\,u_t \,.\end{aligned}

通过一系列的带入和变换，我们发现代价函数变成了$u_t$的显式表达，似乎只有$P_t$是个未知量，但像之前说的，我们的代价函数是从终端往回递归的，我们始终知道t+1时刻的$P_{t+1}$。那么怎么才能找到最优的输入呢？对于这样一个二次型的行驶，当代价函数对输入求导等于0时为最优解，也就是

$$ \frac{\partial V_t(x_t)}{\partial u_t} = 0 $$

将之前得出的$V_t(x_t)$代入可得

$$ 2(R_{t}+B_{t}^TP_{t+1}B_t)u_t +2B_t^TP_{t+1}A_tx_t = 0$$

$$ (R_t + B_t^TP_{t+1}B_t)u_t = -B_t^TP_{t+1}A_tx_t $$

$$ u_t = -{(R_t + B_t^TP_{t+1}B_t)}^{-1}B_t^TP_{t+1}A_tx_t $$

现在我们推导出了每一步的最优控制律的表达式

$$ k_t = {(R_t + B_t^TP_{t+1}B_t)}^{-1}B_t^TP_{t+1}A_t $$

显然我们现在可以在当前时间时刻t利用下一时刻的$P_{t+1}$l来计算当前时刻的最优控制律了，但是我们该如何通过$P_{t+1}$来得到$P_{t}$以计算$u^*_{t-1}$呢？所以我们不得不写出$P_{t}$的迭代表达式。将这个最优控制律，也是就$u^*_t = -kx_t$带入回$V_{t}(x_t)$的表达式中可以得到：

$$ P_t = Q_t + A_t^TP_{t+1}A_t - A^TP_{t+1}B_t(R_t+B^TP_{t+1}B)^{-1}B_t^TP_{t+1}A_t$$

这个方程就是大名鼎鼎的李卡迪方程，因为是讨论有限时域下的收敛问题，所以它是由最终状态N一步一步推演回来的，在此我们可以很简单的发散到无限时域的lqr改如何求解这个P呢？

对于无限时域的lqr来说，我们就无法从终端状态来倒推导P了，我们需要求解一个P的稳态解，也就是当时间趋向于无穷时仍能满足上述李卡迪方程的解：

$$ P = Q + A^TPA - A^TPB(R+B^TPB)^{-1}B^TPA$$

所以对于无限时域lqr来说需要求出李卡迪方程的稳定解，也可以满足我们前面的要求，那么如何计算这个稳定解，依旧需要用到有限时域的解法，只不过这次是从一个假设的初值（假设的无穷时间的终端代价矩阵）开始向前迭代，由于没有了时域的限制，通常我们将两次p矩阵的变化量作为迭代终止的条件。

iLQR推导

有了LQR的基础，我们已经可以解决大部分的问题，但这对于轨迹规划来说远远不够，因为普通的LQR受制与被控对象为线性模型，而在自动驾驶中无论是规划还是控制，无论是运动学模型还是动力学模型都很难用线性模型去飙到，所以ilqr应运而生，让我们重新定义我们要求解的问题：

LaTeX

$$\begin{array}{l}
\min {\substack{u{0}, \ldots, u_{N-1} \
x_{0}, \ldots, x_{N} \
N-1}} J=\frac{1}{2} x_{N}^{T} Q_{N} x_{N}+x_{N}^{T} p_{N}+q_{N} \
+\sum_{k=0}^{N-1}\left(\frac{1}{2} x_{k}^{T} Q x_{k}+x_{k}^{T} p+\frac{1}{2} u_{k}^{T} R u_{k}+u_{k}^{T} r+q\right) \
\text { s.t. } \quad x_{k+1}=f\left(x_{k}, u_{k}\right), \quad k=0,1, \ldots, N-1 \
x_{0}=x^{\text {start }}
\end{array}$$

现在这个最优问题中的等式约束，也就是我们的系统方程变为了非线性方程，要对这样的lqr求解就必须先对这个系统方程进行线性化：

$$ \delta x_{t+1} = A_t\delta x_t + B_t\delta u_t $$

一旦尽心线性化势必会引入线性化的误差，当状态偏离一阶泰勒展开的展开点越远时误差就会越大，而如果只使用线性化的模型+LQR求解，如果初解里最优解较远得到的效果就会很差。不难发现经过一阶泰勒展开后，无论是状态量还是输入量都变成了相对于展开点的delta量，这也是ilqr的整体求解思路，每次迭代都对上一次的解进行delta量的“扰动”使其逐渐收敛至最优值。

现在我们将原本非线性的系统转换为了一个标准的LQR问题：

通过求解这个标准LQR问题可以求得每次“扰动”的delta u并通过每一步进行backward更新系统状态。

带有线性项的LQR问题

在这里还有一个小问题，明显这个LQR问题相比于第一小节提到的LQR问题多了一个一次项（线性项），这该如何求解？其实总体的思路是不变的，而我们最终的输出形式为$u^* = -Kx + w$，其中-Kx为反馈项，这一项与之前的求解无误而w为前馈项。求解过程和之前一致，在这里我大致给出求解的过程：

代价函数为：

$$J = \sum_{k=0}^{N-1} \left( x_k^\top Q x_k + u_k^\top R u_k + c_k^\top x_k + d_k^\top u_k \right) + x_N^\top Q_f x_N + c_N^\top x_N $$

假设 ( V_{k+1}(x_{k+1}) [\latex]具有二次形式：

$$ V_{k+1}(x_{k+1}) = x_{k+1}^\top P_{k+1} x_{k+1} + s_{k+1}^\top x_{k+1} + q_{k+1} $$

其中：

P_{k+1}  是Riccati矩阵（处理二次项），

 s_{k+1}  是线性项的系数向量（处理一次项），

q_{k+1} 是常数项（最终不影响控制律）。

将  V_{k+1}(x_{k+1}) 代入贝尔曼方程：

$$V_k(x_k) = \min_{u_k} \Big[ x_k^\top \left( Q + A^\top P_{k+1} A \right) x_k + u_k^\top \left( R + B^\top P_{k+1} B \right) u_k \\+ u_k^\top \left( 2 B^\top P_{k+1} A x_k + d_k + B^\top s_{k+1} \right) \\+ x_k^\top \left( c_k + A^\top s_{k+1} \right) + \text{常数项} \Big]$$

使V对最优解求导得0为：

$$ \frac{\partial V_k}{\partial u_k} = 2 \left( R + B^\top P_{k+1} B \right) u_k + 2 B^\top P_{k+1} A x_k + d_k + B^\top s_{k+1} = 0$$

$$ u_k^* = - \underbrace{\left( R + B^\top P_{k+1} B \right)^{-1} B^\top P_{k+1} A}_{K_k} x_k - \frac{1}{2} \underbrace{\left( R + B^\top P_{k+1} B \right)^{-1} \left( d_k + B^\top s_{k+1} \right)}_{w_k}$$

CILQR推导

现在对于我们只剩下最后一个问题，这个求解方法还是处理不了约束，这让人很脑瓜子疼因为在自动驾驶中所遇到的约束实在太多了（障碍物、车辆物理约束、交通法规约束），这也就引入了CILQR算法，首先对问题进行建模：

LaTeX

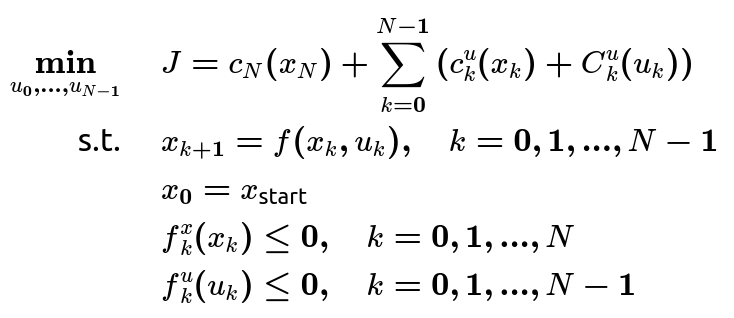
\begin{align*}
\min_{u_0, ..., u_{N-1}} \quad & J = c_N(x_N) + \sum_{k=0}^{N-1} \left( c_k^u(x_k) + C_k^u (u_k) \right) \\
\text{s.t.} \quad & x_{k+1} = f(x_k, u_k), \quad k = 0, 1, ..., N-1 \\
& x_0 = x_{\text{start}} \\
& f_k^x(x_k) \leq 0, \quad k = 0, 1, ..., N \\
& f_k^u(u_k) \leq 0, \quad k = 0, 1, ..., N-1
\end{align*}

这是一个通用的planning问题，其中引入了非线性的cost、constrain以及系统模型（等式约束），好的有了ilqr的求解思路以后这些都不再是困扰我们的问题，由于多次迭代可以使系统逐渐趋近于最优解，那么我们也就不在乎线性化对这些讨厌的非线性问题的影响了，将非线性的cost、constrain线性化，其中对系统方程的线性化同上这里不再赘述。

将非线性cost在x = x_k处进行二阶泰勒展开：

LaTeX

{c}_{k}^{x}\left( {{x}_{k} + \delta {x}_{k}}\right)  \approx  {\left( \delta {x}_{k}\right) }^{T}{\nabla }^{2}{c}_{k}^{x}\left( {x}_{k}\right) \delta {x}_{k} + {\left( \delta {x}_{k}\right) }^{T}\nabla {c}_{k}^{x}\left( {x}_{k}\right)  + {c}_{k}^{x}\left( {x}_{k}\right)

对与constrain我们需要先引入罚函数(障碍函数）的概念，其核心思路在于通过极大的cost惩罚来代替不等式约束

$$b_k^x = q_1\exp (q_2f_k^x)$$

将constrain的非线性函数带入罚函数之后将其也进行线性化：

$$b_k^x \left( x_k + \delta x_k \right) \approx \delta x_k^T \nabla^2 b_k^x \left( x_k \right) \delta x_k + \delta x_k^T \nabla b_k^x \left( x_k \right) + b_k^x \left( x_k \right)$$

这样我们在设计cost以及constrain时只需要给出其嗨森和雅克比矩阵即可。